How to play
MONOID
SETUPYou will need . . . "Elements"
Set out a collection of pieces.

The game will involve manipulating lists of copies of these pieces.
 "Equalities"
"Equalities"
Decide on some lists of pieces to call equal (or interchangeable).
Let's allow these to be swapped out for one another.

And let's allow these all to be swapped out for one another.

The pieces and equalities you set out are just a starting point, and as the game progresses more of them will be created.
INSTRUCTIONSSwapping
From the equalities you have, you can deduce more equalities that were not already known.


To find more lists equal to a particular list, repeatedly swap out contiguous segments for their equals.
Renaming (optional)Any list can be treated as an individual.
Let's use green as shorthand for blue-yellow-red.

At any time for convenience you can introduce a new piece equal to any particular list of existing pieces.
PLAY
See what equalities and pieces can be made from the ones given.
Help
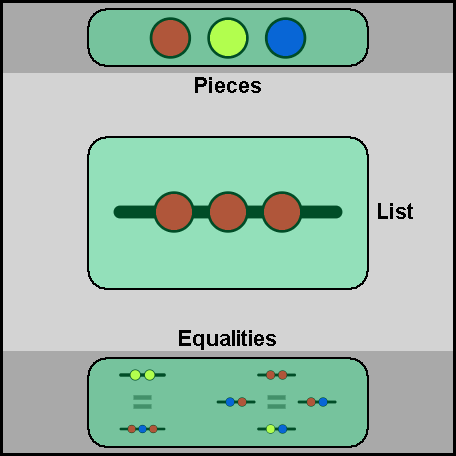
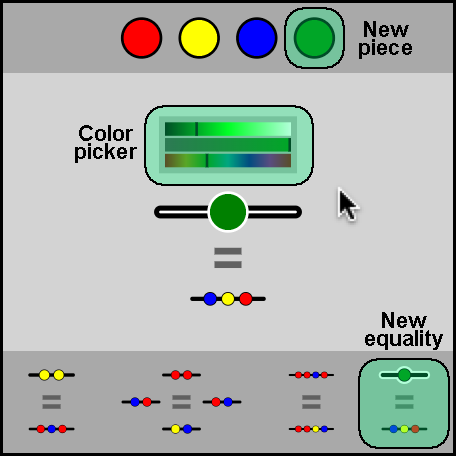
- The upper panel displays the collection of pieces available in this game.
- The lower panel displays the equalities between lists you've discovered.
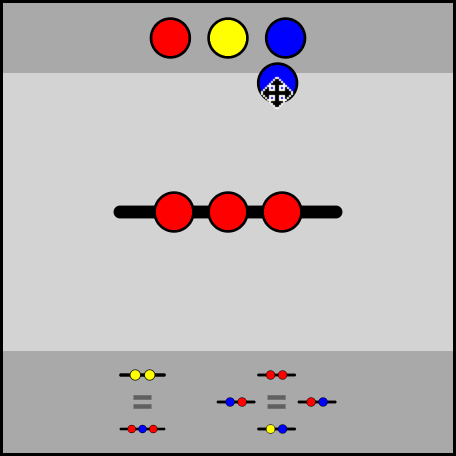
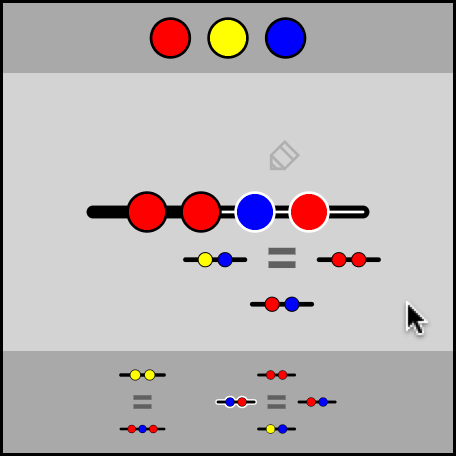
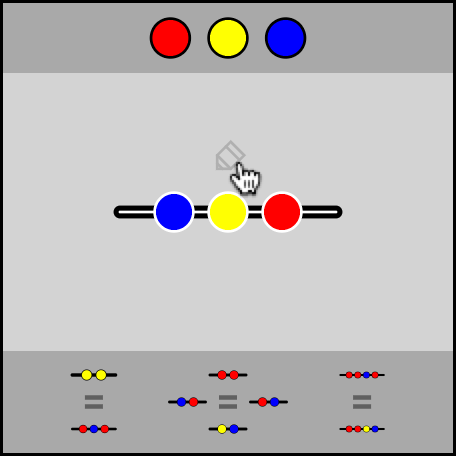
- Drag and drop pieces to and from the center area to build a list.
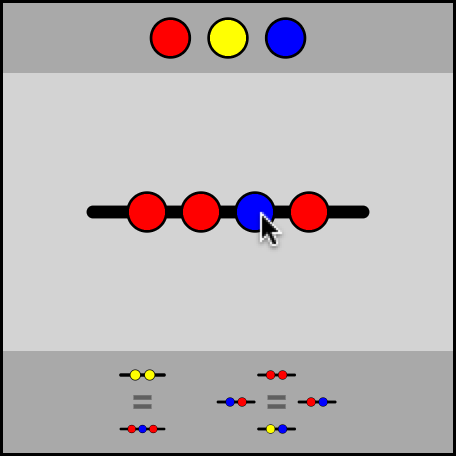
- You can then select parts of this list with your cursor.
- Once a part is selected, anything you've already discovered equal to it will appear next to it.
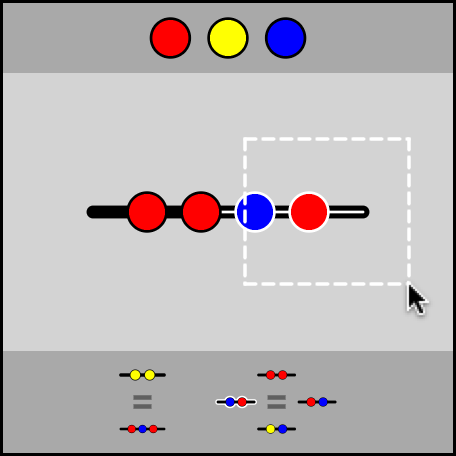
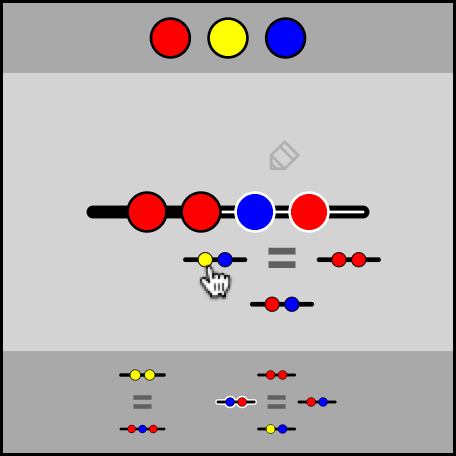
- To find new equalities, swap out equal parts of a list. (Make selections and then click on options that pop up.)
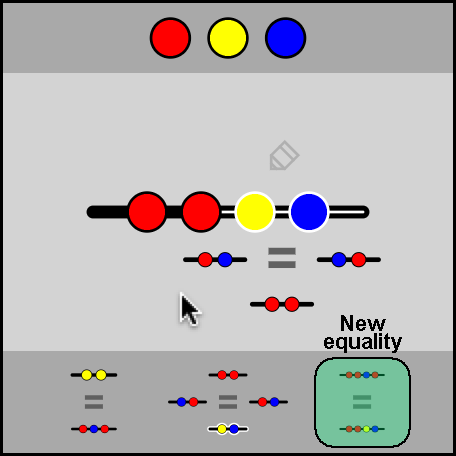
- You can also click the pencil icon next to a selection to rename it, thereby creating a single piece to use as shorthand.
Pro tip: You can hold Control/Command or Shift to make selections with more precision.
VARIATIONS
Without equalities, it's a game of freely making lists.
When "one-way swaps" are used in place of equalities, you get a partially ordered monoid.
| No swapping | Swapping | ||
|---|---|---|---|
 Freely making lists | One-way |  Partially ordered monoid | |
|
Two-way
(equalities) |
 Monoid | ||
If you stop keeping track of the order of pieces in the lists, you get a commutative monoid.
If you furthermore stop keeping track of how many there are of each piece, you get a semilattice.
If rather you keep order but stop counting multiples of the same piece in a row, you get a band.
| (With multiplicity) | |||
|---|---|---|---|
 Semilattice |  Commutative monoid | ||
| (With order) |  Band |  Monoid |
You can make rules restricting which pieces can be placed next to each other in the first place.
If all pieces come with "ends" that must match to join, you get a category.
| No restrictions |
Pieces have "ends"
that have to match up |
Arbitrary restrictions | ||
|---|---|---|---|---|
 Monoid |  Category | Partial monoid |
Instead of a game about swapping out portions of lines, you can play similar games involving other shapes.
| Line | Tree | ... | ... | ... |
|---|---|---|---|---|
 Monoid |  Operad |
Something you can do with a list is flip it backwards. Accordingly, the rules of the game also play well with pieces that can be flipped.
| No flipping |
Flippable pieces and lists |
|---|---|
 Monoid |  Monoid with involution |
SUBTLER VARIATIONS
The ability to rename lists is not an essential part of the game -- you could play without that feature.
Navigate by analogy| No equalities | Swapping |
Multiple arrows
(many "ways of swapping") |
|||
|---|---|---|---|---|---|
|
One-way
swaps |
Equalities
(two-way) |
One-way
arrows |
Two-way
arrows |
||
|
No renaming
(No treating lists as individuals) |
 Free monoid |  Partially ordered monoid with chosen generators |  Monoid with chosen generators |  Colored pro | Colored pro with invertible arrows |
| Renaming allowed |  Partially ordered monoid |  Monoid |  Monoidal category | Monoidal groupoid | |